Deep Learning 101: Transformer Activation Functions Explainer - Sigmoid, ReLU, GELU, Swish
If you read my last post on transformers, you would have seen that activations functions are only briefly mentioned in passing. This post will explain the purpose and use of activation functions, and provide an overview of several popular transformer activation functions. Much of this post will only be relevant if you have prior knowledge on transformers, or have read my previous post.
Overview
Activation functions play an important role in neural networks, including BERT and other transformers. In a transformer model, the activation function is used in the self-attention mechanism to determine the importance of each element in the input sequence. For something often glossed over in tutorials, the choice of activation function can be a make it or break it decision in your neural network setup. With the growth of Transformer based models, different variants of activation functions and GLU (gated linear units) have gained popularity. In this post, we will cover several different activation functions, their respective use cases and pros and cons. While there will be some graphs and equations, this post will try to explain everything in relatively simple terms.
Why use an activation function?
Activation functions are an essential component of neural networks, including transformer models. Activation functions are used to introduce non-linearity into the network, which allows the model to learn and represent complex patterns in the data. Without this, neural networks would only be able to learn linear relationships between the input and output, which would greatly limit their ability to model real-world data. By using an activation function, a neural network can learn complex, non-linear relationships and make more accurate predictions.
What is an Activation Function?
In a neural network, the activation function is the function that governs how the weighted sum of the input in a given layer of the network is transformed into output. Essentially, the activation function defined how and how well the model learns from training data, and what type of predictions the model can make. It follows logically that the activation function applied has quite an impact on the capabilities and performance of a neural network. Luckily, activation functions can be applied to layers within a model so that a network is made capable of performing multiple tasks. While, the activation function is used after each node, neural networks are designed to use the same activation function for all nodes in a layer.
Activation functions are used specifically during the calculations of the values for activations in each layer to decide what the activation value should be. Previous activations are combined with weights and biases in each layer to calculate a value for activations in the next layer, which is then scaled by the activation function before being passed to the next layer.
A network may have three types of layers: input layers that take raw input from the domain, hidden layers that take input from another layer and pass output to another layer, and output layers that make a prediction.
All hidden layers typically use the same activation function. The output layer will typically use a different activation function from the hidden layers and is dependent upon the type of prediction required by the model.
Activation functions are also typically differentiable, meaning the first-order derivative can be calculated for a given input value. This is required given that neural networks are typically trained using the back-propagation of error algorithm that requires the derivative of prediction error in order to update the weights of the model.
There are many different types of activation functions used in neural networks, although perhaps only a small number of functions used in practice for hidden and output layers.
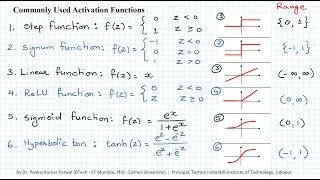
Let’s take a look at some common activation functions and their uses.
scaled dot-product attention function
The scaled dot-product attention function is a type of activation function that is used in transformer models. This function is used in the self-attention mechanism to calculate the importance of each element in the input sequence. The scaled dot-product attention function calculates the dot product of the query and key vectors and scales the result by the square root of the sequence length. This allows the transformer model to weigh the input elements and compute a weighted sum of the values, which is then used to generate the output sequence. The scaled dot-product attention function is a key component of transformer models and allows them to perform well on a wide range of natural language processing tasks.
However, like all activation functions, it has its limitations. One weakness of the scaled dot-product attention function is that it can be computationally expensive, especially when applied to large input sequences. This can make it challenging to use in large-scale applications, such as machine translation or natural language understanding, where the input sequences can be very long. Additionally, the scaled dot-product attention function assumes that the query, key, and value vectors are all the same length, which can limit its ability to model certain types of data. Despite these limitations, the scaled dot-product attention function remains a popular choice for transformer models.
Sigmoid
sigmoid activation function equation
Sigmoid is one of the earliest activation functions used in deep learning. This function takes in a real-valued input and maps it to a value between 0 and 1, which can then be interpreted as a probability. The sigmoid function has a smooth, S-shaped curve, which allows it to model non-linear relationships in the data.
It is often used in binary classification tasks, where the output of the sigmoid function can be interpreted as the probability that an input belongs to a certain class. For example, in a binary classification task with two classes, the sigmoid function can be used to predict the probability that an input belongs to one of the two classes. This can make it an effective tool for tasks such as spam detection, where the goal is to classify an input as either spam or non-spam. Additionally, the sigmoid function can be used in regression tasks, where it can help the network predict a continuous value.
The sigmoid function has been widely used in neural networks, but it has some limitations, such as the vanishing gradient problem, which can make it difficult to train deep networks.
ReLU: Rectified Linear Unit
ReLU Activation Function Equation
In response to the issues with using Sigmoid, ReLU was born and is generally the standard activation function. It’s simple, fast, and works well in many cases.
ReLU is commonly used in feed-forward neural networks. This function takes in a real-valued input and outputs the input if it is positive, and 0 if it is negative.
The ReLU function has several advantages over other activation functions. It is simple to compute, requiring only a single comparison operation, which makes it faster to evaluate than other activation functions. Additionally, the ReLU function does not suffer from the vanishing gradient problem, which can make it easier to train deep networks. Because of these advantages, the ReLU function has become one of the most widely used activation functions in neural networks.
One weakness of ReLU is that it can produce output values that are either 0 or positive, but never negative. This can make it difficult for the network to model data with negative values. Additionally, the ReLU function can suffer from the so-called "dying ReLU" problem, where some of the neurons in the network can become "dead" and stop producing any output. This can happen when the neurons always receive negative input and are therefore always outputting 0, which can make it difficult for the network to learn.
The ReLU function is particularly well-suited for classification tasks, where it can help the network learn to separate different classes of input data. It is also commonly used in deep learning networks, where it can help overcome the vanishing gradient problem and allow the network to learn from large amounts of data. Because of its simplicity and effectiveness, the ReLU function is a popular choice for many applications of neural networks.
GELU: Gaussian Error Linear Unit
GELU Activation Function Qquation
If you combine the effect of ReLU, zone out, and dropout, you get GELU. One of ReLU’s limitations is that it’s non-differentiable at zero - GELU resolves this issue, and routinely yields a higher test accuracy than other activation functions. GELU is now quite popular, and is the activation function used by OpenAI in their GPT series of models.
ReLU vs GelU
tldr: GELU has a smoother, more continuous shape than the ReLU function, which can make it more effective at learning complex patterns in the data.
ReLU and GELU are both continuous and differentiable, which makes them easy to optimize during training. However, there are some key differences between the two functions.
One of the main differences between the ReLU and GELU functions is their shape. The ReLU function is a step function that outputs 0 for negative input values and the input value for positive input values. In contrast, the GELU function has a smooth, bell-shaped curve that is similar to the sigmoid function. This difference in shape can affect the way the two functions behave in different situations.
Another key difference between the ReLU and GELU functions is their behavior when the input values are close to 0. The ReLU function outputs 0 for any input value that is less than or equal to 0, which can make it difficult for the network to learn in these regions. In contrast, the GELU function has a non-zero gradient at x = 0, which allows the network to learn in this region. This can make the GELU function more effective at learning complex patterns in the data.
Swish
Swish was discovered using automatic search methods, specifically with the goal of discovering new activation functions that would perform well. Swish generally performs worse than ReLU in deep learning models - especially for tasks like machine translation.
Swish is, essentially, a smooth function that interpolates between a linear function and ReLU non-linearly. This interpolation is controlled by Swish’s parameter β, which is trainable. Swish is similar to ReLU in some ways - especially as we increase the value of β, but like GELU is differentiable at zero.
Swish Activation Function Equation
The Swish function has a similar shape to the ReLU function, but it is continuous and differentiable, which makes it easier to optimize during training. Additionally, the Swish function has been shown to work well in deep learning networks, where it can help overcome the vanishing gradient problem and improve the network's ability to learn complex patterns in the data. Because of these advantages, the Swish function has gained popularity in recent years and has been used in a number of successful deep learning models.
Since the Swish function is not as well understood as other activation functions, like ReLU or sigmoid , it can be difficult to predict how it will behave in different situations, and it can require more experimentation to determine the optimal settings for a given problem. Additionally, the Swish function has a relatively complex form, which can make it more difficult to compute than other activation functions.
Swish is particularly well-suited for tasks where the network needs to learn complex patterns in the data, such as image or language processing tasks. The Swish function has been shown to perform well in these types of tasks, and it has been used in a number of successful deep learning models. Additionally, the Swish function is well-suited for regression tasks, where it can help the network predict continuous values. Because of its effectiveness in deep learning networks, the Swish function is a popular choice for many applications of neural networks.
Swish vs GeLU
tldr: GELU function has a smoother, more continuous shape than the Swish function, which can make it more effective at learning complex patterns in the data.
The Swish and GELU activation functions are both continuous and differentiable, which makes them easy to optimize during training. However, there are some key differences between the two functions.
One of the main differences between the Swish and GELU functions is their shape. The Swish function is defined as the product of the input value and the sigmoid function, which gives it a smooth, S-shaped curve. In contrast, the GELU function is based on the Gaussian error function, which gives it a smooth, bell-shaped curve. This difference in shape can affect the way the two functions behave in different situations.
Another key difference between the Swish and GELU functions is their behavior when the input values are close to 0. The Swish function has a non-zero gradient at x = 0, which allows the network to learn in this region. However, the GELU function has a much steeper slope near x = 0, which can make it more effective at learning complex patterns in the data. This can make the GELU function a better choice for certain types of tasks, such as natural language processing.
Conclusion
While ReLU is still one of the most popular activation functions, GELU and Swish provide strong alternatives. The fact that we have multiple activation functions speaks to the importance of this choice when building a transformer based model. While we are still far from having the perfect activation function, even for any specific task, this is an evolving area of research.
For a guide through the different NLP applications using code and examples, check out these recommended titles: